Τα ψυχρομετρικά διαγράμματα είναι γραφικές παραστάσεις που δίνουν στους μηχανικούς σύντομες και εύκολες απαντήσεις σε προβλήματα κλιματισμού, χωρίς τη χρησιμοποίηση πολύπλοκων μαθηματικών τύπων της θερμοδυναμικής. Κάθε σημείο αυτών των διαγραμμάτων αντιπροσωπεύει μια συγκεκριμένη κατάσταση του αέρα και δίνουν τη σχέση που υπάρχει ανάμεσα στα φυσικά χαρακτηριστικά, όπως η θερμοκρασία ξηρού και υγρού βολβού, το σημείο δρόσου, η σχετική και η απόλυτη υγρασία, το βάρος του νερού σε κάθε κιλό ή σε κάθε κυβικό μέτρο του αέρα, η ενθαλπία, το ειδικό βάρος, ο ειδικός όγκος κ.α.
Γράφει ο Δημήτρης Μενεγάκης, Μηχανολόγος Μηχανικός
Όταν είναι γνωστά δύο από αυτά τα φυσικά χαρακτηριστικά του αέρα, μπορούμε με απλή αναφορά, χωρίς υπολογισμούς, να προσδιορίσουμε τα υπόλοιπα. Οι μηχανικοί έχουν πάντα στη διάθεσή τους τη θερμοκρασία του ξηρού και του υγρού βολβού του αέρα, που τις προσδιορίζουν εύκολα με το ψυχρόμετρο. Στο προηγούμενο άρθρο μου έδωσα αναλυτική περιγραφή της μεθόδου που χρησιμοποιούμε, για να πάρουμε τις πληροφορίες που ζητούμε από τα διαγράμματα. Ολοκληρώνω, λοιπόν, την απαραίτητη περίληψή μου με μια γρήγορη αναφορά σ’ αυτή τη μέθοδο:
α/ Η κατακόρυφη ευθεία που ξεκινά από τη θερμοκρασία ξηρού βολβού και η πλάγια ευθεία που ξεκινά από τη θερμοκρασία υγρού βολβού, τέμνονται σε ένα σημείο, που δίνει τη σχετική υγρασία του αέρα.
β/ Από το σημείο της σχετικής υγρασίας περνά μια οριζόντια ευθεία, που η μια άκρη της συναντά την καμπύλη κορεσμού και το σημείο τομής δίνει το σημείο δρόσου. Η άλλη άκρη προς τα δεξιά συναντά τον άξονα της απόλυτης υγρασίας. Το σημείο τομής την ποσότητα του νερού σε γραμμάρια ανά κιλό αέρα.
γ/ Από το σημείο της σχετικής υγρασίας περνά και μια πλάγια ευθεία γραμμή, που τέμνει την καμπύλη κορεσμού. Το σημείο τομής δίνει τη θερμοκρασία του υγρού βολβού. Αν αυτή η πλάγια ευθεία επεκταθεί προς τα αριστερά, δίνει την ενθαλπία του αέρα, σε kcal ανά κιλό.
δ/ Σε κάποιες περιπτώσεις προβλημάτων κλιματισμού τα αποτελέσματα δίνονται από τα διαγράμματα ανά κιλό αέρα, ενώ οι μηχανικοί θα προτιμούσαν να το έχουν ανά κυβικό μέτρο. Η μετατροπή είναι απλή. Πολλαπλασιάζετε, επί 1,2 και έχετε αμέσως τα αποτελέσματά σας ανά κυβικό μέτρο, αφού το ειδικό βάρος του αέρα σε κανονικές συνθήκες είναι 1,2 κιλά ανά κυβικό μέτρο. Ύστερα από την παραπάνω απαραίτητη περίληψη του προηγούμενου άρθρου, θα προχωρήσουμε στην επίλυση του πρώτου προβλήματος, που ήταν και η κατάληξη του άρθρου αυτού.
Πρόβλημα 1°
Ατμοσφαιρικός αέρας ανανέωσης θα μπαίνει σε σύστημα κλιματισμού με θερμοκρασία ξηρού βολβού 29⁰C και με σχετική υγρασία 70%. Ο αέρας αυτός θα ψύχεται μέχρι κορεσμού στους 10°C κατά την είσοδό του στο σύστημα. Θέλουμε να υπολογίσουμε το ποσό της θερμότητας, που πρέπει να αφαιρεθεί από τον αέρα (για να ψυχθεί στους 10°C).
Λύση
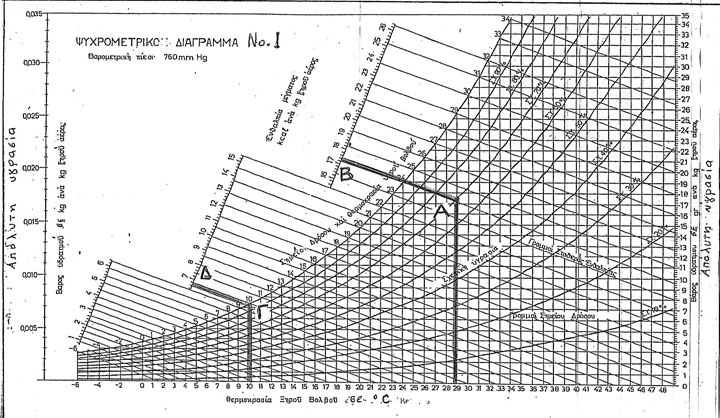
Στο ψυχρομετρικό διάγραμμα Ν₀.1, εντοπίζουμε τη θερμοκρασία ξηρού βολβού 29°C που δόθηκε. Υψώνουμε μια κάθετη ευθεία γραμμή μέχρι να συναντήσουμε την καμπύλη της σχετικής υγρασίας 70% που επίσης δόθηκε στο σημείο τομής Α.
Ακολουθούμε τώρα την πλάγια ευθεία γραμμή που περνά από το Α και στο σημείο Β διαβάζουμε την ενθαλπία του αέρα 17,4 kcal/kg στην κατάσταση αυτή. (Λίγο πριν από το σημείο Β, διαβάζουμε πάνω στην καμπύλη του κορεσμού τη θερμοκρασία υγρού βολβού 24°C. Ο αέρας αυτός πρέπει τώρα να ψυχθεί μέχρι κορεσμού στους 10°C. Πρέπει να βρούμε την ενθαλπία στη νέα κατάσταση. Εργαζόμαστε όπως πριν. Δηλαδή, στο διάγραμμά μας εντοπίζουμε τώρα τη θερμοκρασία ξηρού βολβού 10°C, και υψώνουμε μια κάθετη ευθεία, που συναντά την καμπύλη κορεσμού στο σημείο Γ. Η επέκταση αυτής της πλάγιας ευθείας προς την περιοχή της ενθαλπίας μας δίνει στο σημείο Δ την ενθαλπία 6,8 kcal/kg στην κατάσταση κορεσμού στους 10°C. Η ποσότητα θερμότητας λοιπόν που πρέπει να αφαιρεθεί από τον αέρα, για να ψυχθεί μέχρι κορεσμού στους 10°C είναι η διαφορά θερμότητας ανάμεσα στην αρχική και την τελική κατάσταση, δηλαδή 17,4 – 6,8 = 10,6 kcal/kg ή 10,6 x 1,2 = 12,72 kcal/m³. Βρήκαμε χωρίς υπολογισμούς, ότι κάθε κυβικό μέτρο αέρα της ανανέωσης για να ψυχθεί στους 10°C πρέπει να αφαιρούμε 12,72 kcal. Αν για παράδειγμα ο αέρας της ανανέωσης είναι 3000 m³ ανά ώρα, τότε η ολική θερμότητα που πρέπει να αφαιρείται είναι 12,72 x 3000 = 38160 kcal/h
Μια αξιοπρόσεκτη παρατήρηση. Όταν ο αέρας είναι σε κατάσταση κορεσμού, δηλαδή όταν η σχετική του υγρασία είναι 100%, τότε η θερμοκρασία ξηρού βολβού, η θερμοκρασία υγρού βολβού και η θερμοκρασία του σημείου δρόσου είναι ίδια. Αυτό σημειώνεται και στο πρόβλημά μας. Όταν σε κατάσταση κορεσμού η θερμοκρασία ξηρού βολβού είναι 10°C, τότε και η θερμοκρασία υγρού βολβού είναι 10°C (σημείο Γ), καθώς και το σημείο δρόσου είναι 10°C, πάνω στην καμπύλη κορεσμού.
Πρόβλημα 2°
Σε εγκατάσταση κλιματισμού μιας βιομηχανίας θα μπαίνει ατμοσφαιρικός αέρας ανανέωσης 4000 m³/h, με θερμοκρασία ξηρού βολβού 0°C και με σχετική υγρασία 70%. Ο αέρας αυτός θα θερμαίνεται στους 21°C και θα κυκλοφορεί στο σύστημα με σχετική υγρασία 50%. Κατά τη θέρμανση όμως ελαττώνεται σημαντικά η σχετική υγρασία, οπότε απαιτείται ύγρανση. Θέλουμε να υπολογίσουμε την ποσότητα του νερού που πρέπει να ψεκάζουμε στον αέρα, για να πετύχουμε τη ζητούμενη σχετική υγρασία (50%). Με άλλα λόγια, ζητούμε την ωριαία παροχή του υγραντή.
Λύση
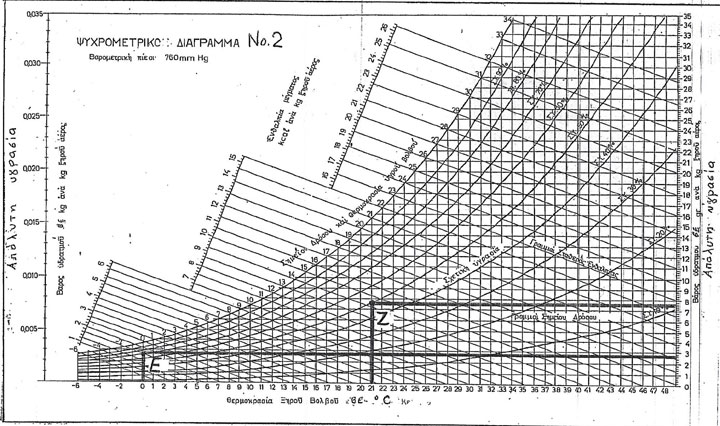
Στο ψυχρομετρικό διάγραμμα Ν°2 εντοπίζουμε τη θερμοκρασία 0°C που μας δόθηκε. Υψώνουμε μια κατακόρυφη ευθεία, που συναντά στο σημείο Ε την καμπύλη της σχετικής υγρασίας 70%, που επίσης μας δόθηκε. Το σημείο Ε αποτυπώνει την αρχική κατάσταση του αέρα, όταν μπαίνει στο σύστημα. Στην κατάσταση αυτή η απόλυτη υγρασία είναι 2,6 γραμμάρια ανά κιλό αέρα, όπως δείχνει η οριζόντια ευθεία που σύρεται από το Ε προς τον άξονα της απόλυτης υγρασίας. Το σημείο Ζ είναι το σημείο που συναντά η κατακόρυφη ευθεία της θερμοκρασίας 21°C την καμπύλη της σχετικής υγρασίας 50% και αποτυπώνει την τελική κατάσταση του αέρα, όταν έχει πλέον κλιματιστεί στις απαιτούμενες συνθήκες, για να κυκλοφορήσει στο σύστημα.
Στην κατάσταση αυτή η απόλυτη υγρασία του αέρα είναι 7,6 γραμμάρια ανά κιλό, όπως δείχνει η οριζόντια ευθεία που σύρεται από το Ζ προς τον άξονα της απόλυτης υγρασίας. Είναι προφανές ότι η διαφορά της απόλυτης υγρασίας ανάμεσα στην αρχική και την τελική κατάσταση δίνει την ποσότητα του νερού, που πρέπει να ψεκάζεται στον αέρα, δηλαδή 7,6 – 2,6 = 5 γραμμάρια ανά κιλό, ή 5 x 1,2 = 6 γραμμάρια ανά κυβικό μέτρο αέρα. Γνωρίζοντας την ποσότητα του αέρα, που κυκλοφορεί βρίσκουμε εύκολα την ποσότητα του νερού που πρέπει να ψεκάζουμε και είναι 4000 x 6 = 24000 γραμμάρια ανά ώρα = 24 κιλά ανά ώρα. Αυτή είναι και η παροχή του υγραντή μας.
Πρόβλημα 3 °
Ατμοσφαιρικός αέρας του περιβάλλοντος θερμοκρασίας ξηρού βολβού 19°C και σχετικής υγρασίας θα ανακυκλοφορεί σε σύστημα κλιματισμού, αφού πρώτα θα κλιματίζεται στις συνθήκες του συστήματος που είναι θερμοκρασία ξηρού βολβού 24°C και σχετική υγρασία 40%. Ζητούνται:
α/ Σε τι θερμοκρασία κορεσμού πρέπει να ψυχτεί ο αέρας για να πέσει η σχετική του υγρασία στο 40%.
β/ Το ποσό της θερμότητας που πρέπει να αφαιρεθεί για να πέσει η θερμοκρασία του αέρα στη θερμοκρασία της αφύγρανσης.
γ/ Το ποσό της θερμότητας που πρέπει να δαπανάται για την αναθέρμανση του αέρα στους 24°C.









