Για να συνδεθούμε με τα προηγούμενα θα ήθελα να υπενθυμίσω, ότι το θέμα μου θα αναπτυχτεί με συμπυκνωμένες σημειώσεις, σε πέντε ενότητες. Η πρώτη ενότητα αναφέρθηκε στο τεύχος 69 του περιοδικού μας, η δεύτερη στο τεύχος 70 και στο τεύχος 71 η Τρίτη ενότητα που περιλαμβάνει τη μελέτη ενός δικτύου αεραγωγών καθώς και τη μελέτη των αντιστάσεων στη ροή του αέρα μέσα στους αεραγωγούς αυτούς, δηλαδή την πτώση της πίεσης, αλλά και τις μεθόδους που υιοθετούνται για να ελαττωθούν στο ελάχιστο δυνατό αυτές οι αντιστάσεις ροής, που σημαίνει την αύξηση της απόδοσης ολόκληρου του συστήματος.
Γράφει ο Δημήτρης Μενεγάκης
Μηχανολόγος Μηχανικός
8. Ροή του αέρα μέσα σε αεραγωγούς
Για να υπάρχει ροή αέρα μέσα σε ένα αεραγωγό, πρέπει να υπάρχει μια διαφορά πίεσης ανάμεσα στην είσοδο και την έξοδο. Πρέπει να υπάρχει μια πίεση ροής, που την εξασφαλίζει ο ανεμιστήρας του συστήματος.
Πίεση ροής του αέρα.
Στατική-Δυναμική και Ολική πίεση
Όταν ο αέρας κινείται μέσα σε ένα αεραγωγό, διακρίνουμε τρείς πιέσεις:
- Τη στατική ή μανομετρική
- Τη δυναμική και
- Την ολική πίεση, που είναι το άθροισμα των δύο προηγούμενων, δηλαδή της στατικής και της δυναμικής, που είναι η πίεση κατάθλιψης του ανεμιστήρα.
Η στατική πίεση εξασκείται από τον αέρα κάθετα στα τοιχώματα του αεραγωγού, προς μια κατεύθυνση δηλαδή που σχηματίζει γωνία 90⁰ με την κίνησή του, όπως δείχνει το σκαρίφημα 1.
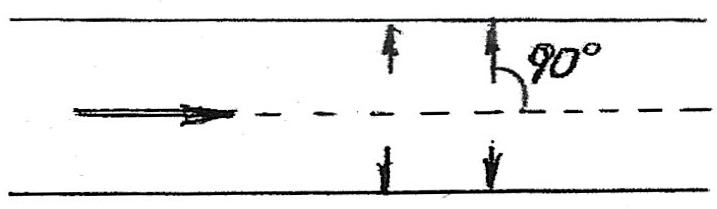
Σκαρίφημα 1
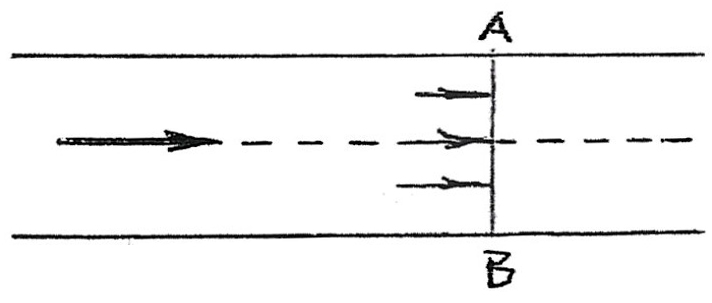
Η δυναμική πίεση εξασκείται από τον αέρα κάθετα σε ένα επίπεδο ΑΒ, που είναι κάθετο προς την κίνησή του, όπως δείχνει το σκαρίφημα 2.
Η ολική πίεση είναι το άθροισμα της στατικής και της δυναμικής πίεσης. Αυτή είναι η πίεση ροής. Πρακτικά η πίεση ροής του αέρα μέσα σε ένα αεραγωγό είναι το άθροισμα της μανομετρικής πίεσης και της πίεσης κατάθλιψης του ανεμιστήρα.
Είναι αξιοσημείωτο αυτό που συμβαίνει με τις δύο αυτές πιέσεις του αέρα. Αν κάποια αιτία προκαλέσει ελάττωση της μιας, τότε η ίδια αιτία θα προκαλέσει αύξηση της άλλης, έτσι ώστε το άθροισμά τους θα παραμείνει σταθερό. Αν για παράδειγμα κάποια αιτία προκαλέσει ελάττωση της στατικής πίεσης του αέρα μέσα στον αεραγωγό, τότε η ίδια αιτία θα προκαλέσει αύξηση της δυναμικής πίεσης, έτσι ώστε το άθροισμά τους, δηλαδή η ολική πίεση θα παραμένει σταθερό.
Το σκαρίφημα 3 είναι μια εικονογραφημένη επεξήγηση αυτού του σημαντικού φαινομένου.
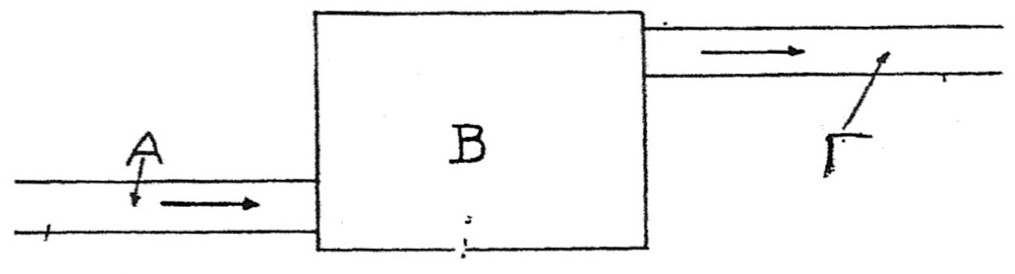
Σκαρίφημα 3
Ο αεραγωγός Α έχει μικρή διατομή. Εδώ ο αέρας αναπτύσσει μεγάλη ταχύτητα. Η στατική πίεση είναι χαμηλή, ενώ η δυναμική είναι μεγάλη. Ο αέρας μπαίνει στη συνέχεια στον αεραγωγό Β, που έχει μεγάλη διατομή. Εδώ η ταχύτητα του αέρα χαμηλώνει. Η δυναμική πίεση επίσης χαμηλώνει, ενώ η στατική πίεση του αέρα αυξάνεται. Τώρα ο αέρας μπαίνει μέσα στον αεραγωγό Γ, που έχει μικρή διατομή. Η ταχύτητα του αέρα θα μεγαλώσει. Θα μεγαλώσει επίσης και η δυναμική πίεση, ενώ αντίθετα η στατική πίεση θα ελαττωθεί. Και στις τρείς όμως περιπτώσεις, μέσα στα τμήματα Α,Β και Γ του αεραγωγού η ολική πίεση θα είναι ίδια, εφ’ όσον αυτή είναι το άθροισμα της δυναμικής και της στατικής πίεσης. Και στα τρία λοιπόν τμήματα του αεραγωγού θα έχουμε την ίδια πίεση ροής.
Η απώλεια της πίεσης ροής (ή πτώση πίεσης)
Όταν ο αέρας κινείται μέσα σε ένα αεραγωγό προκαλούνται διάφορες αντιστάσεις στη ροή, που έχουν σαν αποτέλεσμα την ελάττωση της πίεσης ροής του αέρα. Όταν όμως ελαττώνεται η πίεση ροής ελαττώνεται και η ποσότητα του αέρα που θα περνά από τον αεραγωγό, δηλαδή ελαττώνεται η παροχή σε μια χρονική περίοδο.
Οι κύριοι παράγοντες της ελάττωσης της πίεσης ροής είναι:
- Οι τριβές του αέρα στα τοιχώματα του αεραγωγού
- η ανώμαλη ροή στα διάφορα σημεία του δικτύου, που προκαλεί στραγγαλισμούς, στροβιλισμούς και περιδινήσεις.
Για την τριβή του αέρα πάνω στα τοιχώματα του αεραγωγού πρέπει να ξεκαθαρίσουμε μερικά θέματα:
α/ Η τριβή είναι ανάλογη με το μήκος του δικτύου των αεραγωγών, που σημαίνει ότι όσο μεγαλώνει το μήκος του δικτύου, τόσο μεγαλώνει και η τριβή.
β/ Η τριβή είναι ανάλογη με την ταχύτητα του αέρα, που σημαίνει ότι όσο μεγαλώνει η ταχύτητα, τόσο μεγαλώνει και η τριβή. Στην προκείμενη περίπτωση είναι πιο γνωστή με την ονομασία “πίεση ταχύτητας” που θα εξηγηθεί στο κεφάλαιο 9.
γ/ Η τριβή όμως είναι αντίστροφα ανάλογη με τη διατομή του αεραγωγού, δηλαδή όσο μεγαλώνει η διατομή τόσο μικραίνει η τριβή και όσο μικραίνει η διατομή, τόσο μεγαλώνει η τριβή. Όταν όμως μεγαλώνει η τριβή μεγαλώνει και η αντίσταση στη ροή του αέρα.
Για την ανώμαλη ροή του αέρα στα διάφορα σημεία του δικτύου που προκαλούν στραγγαλισμούς και στροβιλισμούς που έχουν σαν αποτέλεσμα την ελάττωση της πίεσης ροής, πρέπει να παρατηρήσουμε:
α/ Εξαρτήματα όπως γωνίες, Τ διακλαδώσεων, συστολές, φίλτρα, τάμπερ κλπ. Προκαλούν ελάττωση της πίεσης ροής και πρέπει να χρησιμοποιούνται με μεγάλη σχολαστικότητα.
β/ Τα απότομα στενέματα της διατομής του αεραγωγού, οι διακλαδώσεις, τα σημεία αλλαγής της διεύθυνσης της ροής, αεροψυκτήρες κλιματισμού κλπ. Το άθροισμα των απωλειών πίεσης όλων αυτών των εξαρτημάτων μας δίνει τη συνολική απώλεια πίεσης που χαρακτηρίζει τη συνολική αντίσταση στη ροή του αέρα μέσα στους αεραγωγούς. Είναι αυτή η απώλεια πίεσης, που πρέπει να προσέχουμε ιδιαίτερα, όταν ασχολούμαστε με τη μελέτη ενός συστήματος αεραγωγών. Για να αποφεύγεται η ανώμαλη ροή του αέρα χρησιμοποιούνται εξαρτήματα ή τμήματα αεραγωγών χωρίς απότομα στενέματα ή απότομες αλλαγές στη διεύθυνση ροής του αέρα με ορισμένες αναλογίες, που δείχνουν τα πιο κάτω σκαριφήματα:
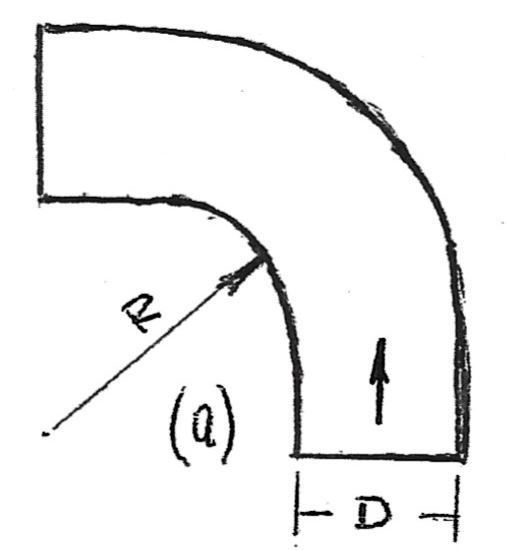
Σκαρίφημα α
Σκαρίφημα (α) Η ανοιχτή γωνία (α) έχει αναλογία ![]() = 2 δηλαδή η καμπυλότητας R είναι διπλάσια της διαμέτρου D. Παρουσιάζει 40% βελτίωση της απώλειας πίεσης από μια άλλη πιο κλειστή γωνιά με αναλογία
= 2 δηλαδή η καμπυλότητας R είναι διπλάσια της διαμέτρου D. Παρουσιάζει 40% βελτίωση της απώλειας πίεσης από μια άλλη πιο κλειστή γωνιά με αναλογία ![]() = ¼
= ¼
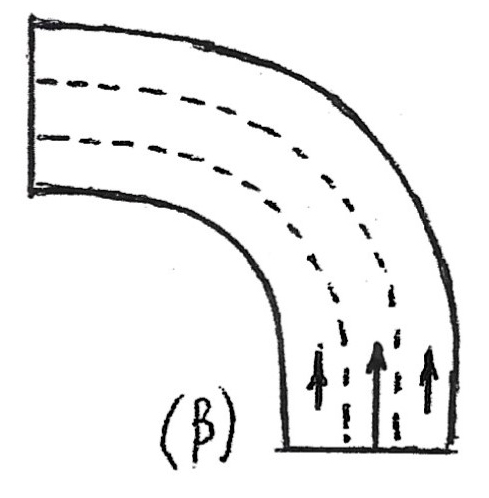
Σκαρίφημα β
Σκαρίφημα (β) Η γωνία (β) έχει τις ίδιες αναλογίες με την (α) δηλαδή
![]() = 2. Έχουν όμως τοποθετηθεί δύο οδηγητικά πτερύγια που δείχνουν οι διακεκομμένες γραμμές. Η ροή του αέρα είναι ακόμη πιο ομαλή και παρουσιάζει 30% βελτίωση της απώλειας πίεσης σε σχέση με την (α).
= 2. Έχουν όμως τοποθετηθεί δύο οδηγητικά πτερύγια που δείχνουν οι διακεκομμένες γραμμές. Η ροή του αέρα είναι ακόμη πιο ομαλή και παρουσιάζει 30% βελτίωση της απώλειας πίεσης σε σχέση με την (α).
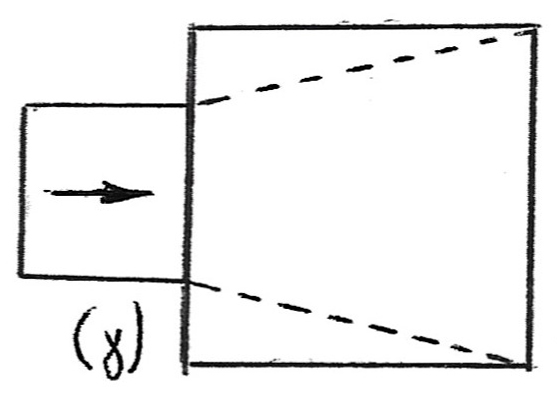
Σκαρίφημα γ
Σκαρίφημα (γ) Ένας αεραγωγός με μικρή διατομή συνδέεται με άλλον μεγαλύτερης διατομής. Αν η σύνδεση πάρει την κωνική μορφή που δείχνει η διακεκομμένη γραμμή, τότε προκύπτει βελτίωση 25% της απώλειας πίεσης.
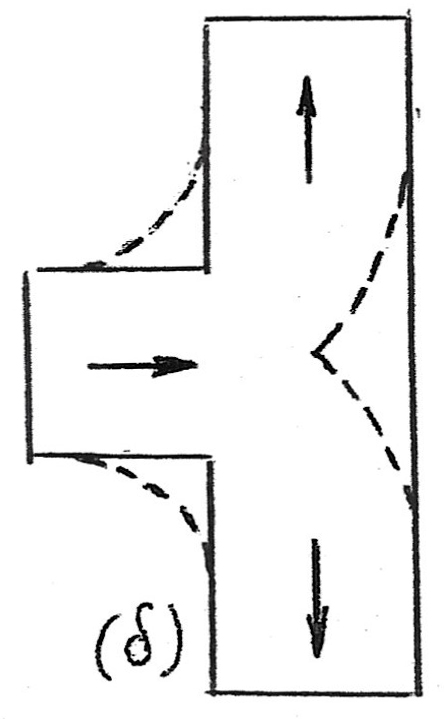
Σκαρίφημα δ
Σκαρίφημα (δ) Το “Τ” του σχήματος (δ) παρουσιάζει 40% βελτίωση της απώλειας πίεσης, αν πάρει τη μορφή που δείχνει η διακεκομμένη γραμμή.
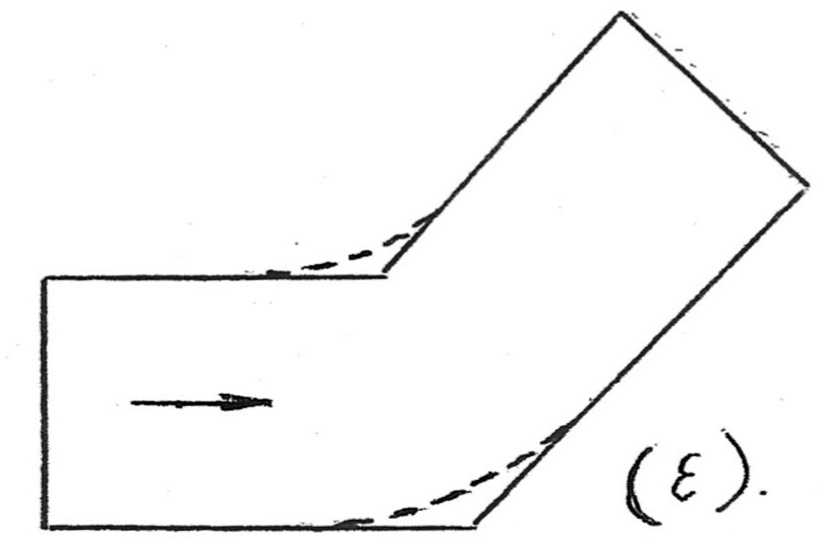
Σκαρίφημα ε
Σκαρίφημα (ε) Η γωνία 45° του σχήματος (ε) παρουσιάζει 20% βελτίωση της απώλειας πίεσης, αν πάρει τη μορφή που δίνουν οι διακεκομμένες γραμμές.
9. Η πίεση ταχύτητας του αέρα
Στο κεφάλαιο 8 αναφέρθηκε, ότι όσο μεγαλώνει η ταχύτητα του αέρα μέσα σε ένα αεραγωγό, τόσο μεγαλώνει και η τριβή πάνω στα τοιχώματα, δηλαδή η αντίσταση στη ροή του αέρα. Αυτή η τριβή ονομάζεται “πίεση ταχύτητας” επειδή προέρχεται από την ταχύτητα.
Σε κάθε ταχύτητα του αέρα αναλογεί μια πίεση ταχύτητας, που φαίνεται στο κάτω διάγραμμα.
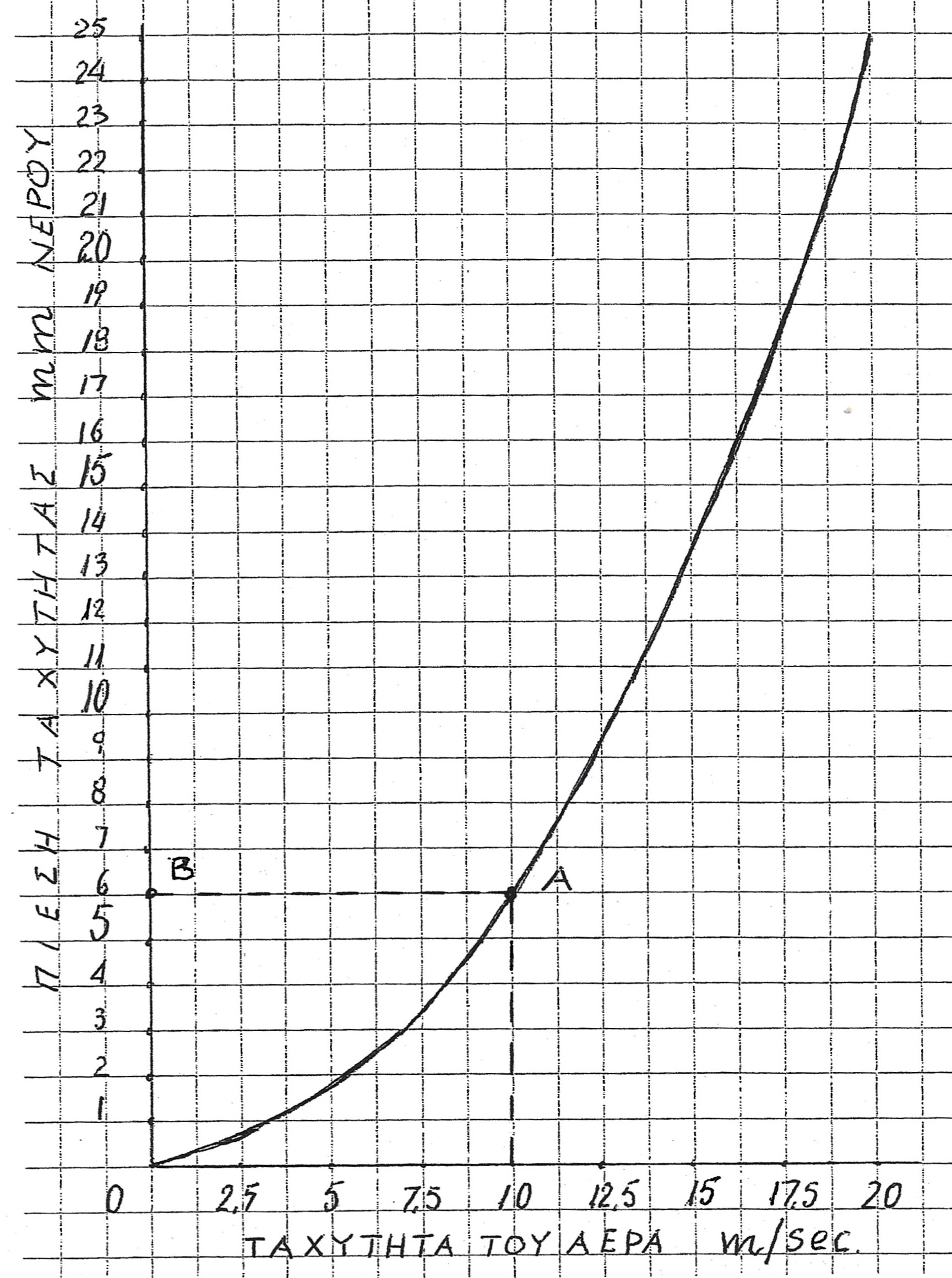
Η πίεση ταχύτητας χρησιμεύει στους υπολογισμούς της απώλειας πίεσης των εξαρτημάτων του δικτύου των αεραγωγών, δηλαδή Γωνίες, Τα διακλαδώσεις, τάμπερ, φίλτρα, συστολές κλπ. Θα δούμε στο κεφάλαιο 15 ότι βρίσκουμε την απώλεια πίεσης των εξαρτημάτων σαν ποσοστό της πίεσης ταχύτητας, που μας δίνει το διάγραμμα.
Περιγραφή του Διαγράμματος
Αποτελείται από ένα κατακόρυφο άξονα, πάνω στον οποίο σημειώνεται η πίεση ταχύτητας σε mm στήλης νερού και ένα οριζόντιο άξονα, πάνω στον οποίο σημειώνεται η ταχύτητα του αέρα σε m/sec. Η καμπύλη αφορά αέρα ατμοσφαιρικό, σε κανονικές συνθήκες, δηλαδή θερμοκρασία 21°C και βαρομετρική πίεση 1atm (760mm. Υδραργύρου)
Χρήση του Διαγράμματος
Όταν μας είναι γνωστή η ταχύτητα του αέρα μέσα στον αεραγωγό (βλέπε κεφάλαιο 10), την εντοπίζουμε πάνω στον οριζόντιο άξονα του διαγράμματος. Υψώνουμε μια κατακόρυφη ευθεία μέχρι να συναντήσουμε την καμπύλη. Αυτό το σημείο τομής τραβούμε μια κάθετη ευθεία γραμμή στον κατακόρυφο άξονα και εκεί διαβάζουμε την πίεση ταχύτητας.
Παράδειγμα
Αν η ταχύτητα του αέρα μέσα σε ένα αεραγωγό είναι 10m/sec τι πίεση ταχύτητας αναλογεί σ’ αυτήν;
Εντοπίζουμε στον οριζόντιο άξονα την ταχύτητα 10m/sec. Υψώνουμε μια κατακόρυφη ευθεία μέχρι να συναντήσουμε την καμπύλη (Α). Από το Α τραβούμε μια κάθετη γραμμή και στο σημείο Β, πάνω στον κατακόρυφο άξονα διαβάζουμε 6 mm νερού. Έτσι απλά χωρίς υπολογισμούς. Σε μερικές περιπτώσεις μας δίδεται η ταχύτητα του αέρα σε χιλιόμετρα ανά ώρα. Για να χρησιμοποιήσουμε το διάγραμμά μας πρέπει να τη μετατρέψουμε σε m/sec. Σαν παράδειγμα, μας δίνουν την ταχύτητα του αέρα μέσα στον αεραγωγό να είναι 54 χιλιόμετρα την ώρα. Η μετατροπή είναι εύκολη, και είναι 54km = 54000 m/ώρα (δηλαδή σε 3600 δευτερόλεπτα) 54000:3600 = 15 m/sec.
10. Η ταχύτητα ροής του αέρα μέσα στους αεραγωγούς
Η ποσότητα του αέρα που θα περάσει μέσα από έναν αεραγωγό είναι ανάλογη με την ταχύτητα. Όσο αυξάνεται η ταχύτητα του αέρα, τόσο θα αυξάνεται και η παροχή του αεραγωγού.
Η αύξηση της ταχύτητας έχει κάποια όρια, πάνω από τα οποία δημιουργούνται ορισμένα σοβαρά προβλήματα, τα κυριότερα από τα οποία είναι:
—ο θόρυβος και
—η πίεση ταχύτητας του αέρα, που είδαμε στο κεφάλαιο 9.
Στον πίνακα 1 φαίνονται οι “παραδεκτές” ταχύτητες του αέρα μέσα στους αεραγωγούς, ανάλογα με τον προορισμό του αεραγωγού και του χώρου. Οι αριθμοί μέσα στις παρενθέσεις είναι ταχύτητες σε m ανά δευτερόλεπτο (m/sec).
| Είδος αεραγωγού | Πίνακας 1. Παραδεκτή ταχύτητα αέρα σε m/h | |||
| Κατοικίες, Βιβλιοθήκες Νοσοκομεία, Γραφεία (1) |
Γραφεία (2), Σχολεία, Εκκλησίες, Ξενοδοχεία, Εστιατόρια |
Βιομηχανικοί χώροι, Συνεργεία |
Studios TV, Ραδιοφώνου, Θέατρα |
|
| Κεντρικός | 1800 (5) | 24000 (6,7) | 36000 (10) | 9000 (2,5) |
| Κλάδος διανομής | 15000 (4,2) | 18000 (5) | 33000 (9,2) | 9000 (2,5) |
| Κατακόρυφος | 13000 (3,6) | 15000 (4,2) | 27000 (7,5) | 9000 (2,5) |
| Εξωτερικού αέρα | 15000 (4,2) | 16000 (4,5) | 22000 (6) | 9000 (2,5) |
| Ανακυκλοφορία | 14000 (3,9) | 18000 (5) | 27000 (7,5) | 9000 (2,5) |
| Έξοδος ανεμιστήρα | 27000 (7,5) | 33000 (9,2) | 36000 (10) | 27000 (7,5) |
Ιδιαίτερα για τα δίκτυα εξαερισμού αναφέρονται στον πιο κάτω πίνακα οι ελάχιστες απαιτούμενες ταχύτητες του αέρα κοντά στα σημεία γένεσης, για να παρασυρθούν οι οσμές:
| Ατμοί, αναθυμιάσεις, κουζίνες | 9000m/h (2,5m/sec) |
| Ψησταριές, εργαστήρια, συνεργεία | 15000m/h (4,2m/sec) |
| Βαφεία, σιδηρουργεία, ηλεκτροσυγκολλήσεις | 24000m/h (6,7m/sec) |
| Χυτήρια | 33000m/h (9,2m/sec) |
| Αμμοβολές, τροχεία | 72000m/h (20m/sec) |
11. H μελέτη Δικτύου Αεραγωγών – Υπολογισμός των στοιχείων ενός Αεραγωγού.
Τα κύρια στοιχεία ενός αεραγωγού είναι:
- Ο όγκος του αέρα που θα κινείται μέσα στον αεραγωγό (παροχή)
- Η ταχύτητα ροής του αέρα
- Η διατομή και
- Η αντίσταση που παρουσιάζει ο αεραγωγός στην κίνηση του αέρα.
Όταν εκπονούμε τη μελέτη ενός αεραγωγού, ασχολούμαστε με τον υπολογισμό των τεσσάρων στοιχείων του, που αναφέρθηκαν πιο πάνω.
Έτσι:
- Ο όγκος του αέρα που θα διακινείται, δηλαδή η παροχή του αεραγωγού μας είναι πάντα γνωστή ή μας γίνεται γνωστή με τη μέθοδο που αναπτύχθηκε στο κεφάλαιο 5
- Η ταχύτητα ροής του αέρα μέσα στον αεραγωγό μας είναι πάντα γνωστή, αφού επιλέγεται από εμάς, από τον πίνακα του κεφαλαίου 10
- Η διατομή του αεραγωγού και η μέθοδος υπολογισμού της θα αναφερθεί στο αμέσως επόμενο κεφάλαιο 12, και
- Η αντίσταση που παρουσιάζει ο αεραγωγός στη ροή του αέρα και η μέθοδος υπολογισμού της, θα αναφερθεί στο κεφάλαιο 13
12. Υπολογισμός της Διατομής ενός Αεραγωγού
Η διατομή ενός αεραγωγού βρίσκεται με τον τύπο F = ![]()
Στον οποίο
F = διατομή του αεραγωγού σα m²
Q = παροχή σε m³/h ή m³/sec
T = ταχύτητα του αέρα σε m/h ή σε m/sec
Αξίζει να επαναλάβουμε ότι όταν εκπονούμε τη μελέτη ενός αεραγωγού γνωρίζουμε πάντα την παροχή Q ή την προσδιορίζουμε με τη μέθοδο που αναφέρθηκε στο κεφάλαιο 5, γνωρίζουμε ακόμα και την ταχύτητα Τ του αέρα που μας δίνει ο πίνακας του κεφαλαίου 10.
Εκείνο που πρέπει να προσέξουμε είναι η παροχή Q και η ταχύτητα Τα να είναι σε αντίστοιχες μονάδες, δηλαδή αν η παροχή εκφράζεται σε m³/h, τότε η ταχύτητα Τα πρέπει και αυτή να μπει στον τύπο σε m/h. Αν πάλι η ταχύτητα εκφράζεται σε m/sec τότε η παροχή πρέπει να μπει στον τύπο σε m³/sec. Πρέπει να σημειώσουμε ακόμη μια λεπτομέρεια. Η διατομή του αεραγωγού F, όπως θα την υπολογίσουμε είναι m². Αν θέλουμε να τη μετατρέψουμε σε cm², τότε πρέπει να πολλαπλασιάσουμε επί 10.000.
Παράδειγμα
Αναφερόμαστε πάλι στο παράδειγμα του κεφαλαίου 5, στο οποίο είχαμε υπολογίσει την παροχή του συστήματος αερισμού της αίθουσας ενός εστιατορίου Q = 10.000 m³/h. Για το ίδιο παράδειγμα ζητούμε τώρα να υπολογίσουμε τη διατομή του κεντρικού αεραγωγού.
Η διατομή του αεραγωγού θα υπολογιστεί με τον τύπο
F = ![]()
Η παροχή μας είναι γνωστή Q =10.000 m³/h
Η ταχύτητα μας είναι άγνωστη. Για να την προσδιορίσουμε θα πάμε στον πίνακα του κεφαλαίου 10, εκεί θα δούμε ότι η ταχύτητα στον αέρα μέσα στον κεντρικό αεραγωγό ενός εστιατορίου πρέπει να είναι 24000 m/h ή 6,7 m/sec. Επειδή η παροχή μας δόθηκε σε m³/h, είμαστε υποχρεωμένοι να χρησιμοποιήσουμε για την ταχύτητα m/h. Έχουμε λοιπόν
F =![]() =
=![]() = 0,4167 m²
= 0,4167 m²
Αν θέλουμε τα m² της διατομής να τα κάνουμε cm² θα πολλαπλασιάσουμε επί 10.000 και έχουμε
F =0,4167m² = 0,4167 x 10.000 = 4167 cm²
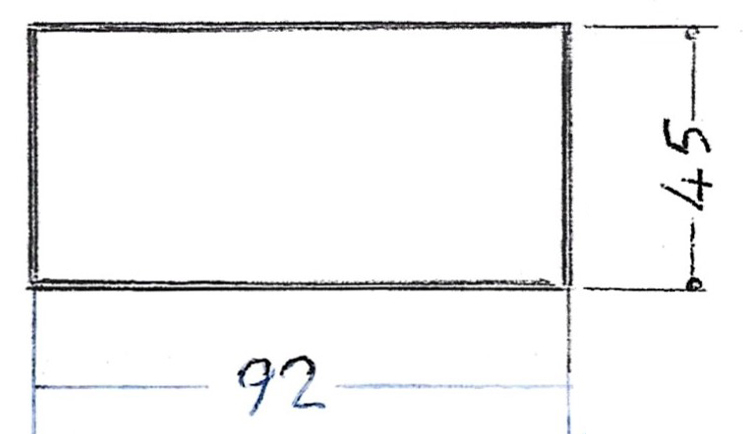
Και οι διαστάσεις της ορθογωνικής διατομής θα είναι cm: